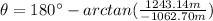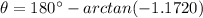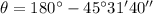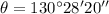Answer:
- magnitude : 1635.43 m
- Angle: 130°28'20'' north of east
Step-by-step explanation:
First, we will find the Cartesian Representation of the
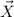 and
and
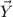 vectors. We can do this, using the formula
vectors. We can do this, using the formula
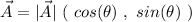
where
 its the magnitude of the vector and θ the angle. For
its the magnitude of the vector and θ the angle. For
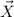 we have:
we have:
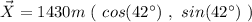
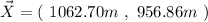
where the unit vector
 points east, and
points east, and
 points north. Now, the
points north. Now, the
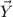 will be:
will be:
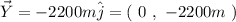
Now, taking the sum:
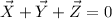
This is
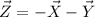
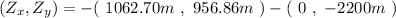
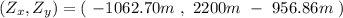
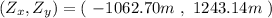
Now, for the magnitude, we just have to take its length:
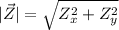
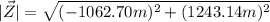
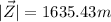
For its angle, as the vector lays in the second quadrant, we can use: