Answer:
n = 5 approx
Step-by-step explanation:
If v be the velocity before the contact with the ground and v₁ be the velocity of bouncing back
 = e ( coefficient of restitution ) =
= e ( coefficient of restitution ) =
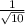
and
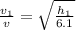
h₁ is height up-to which the ball bounces back after first bounce.
From the two equations we can write that
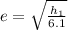
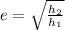
So on
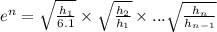
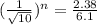 = .00396
= .00396
Taking log on both sides
- n / 2 = log .00396
n / 2 = 2.4
n = 5 approx