Answer:
The proof makes use of congruences as follows:
Explanation:
We can prove this result using congruences module 3. First of all we shall show that
 for all
for all
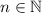 . By induction we have
. By induction we have
 . For
. For
 we have
we have

- Suppose that the statement is true for
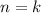 and let's prove that it is also true for
and let's prove that it is also true for
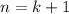 . In fact,
. In fact,

Then induction we proved that
 for all
for all
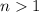 . Then
. Then
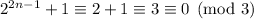
From here we conclude that the expression
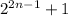 is divisible by 3.
is divisible by 3.