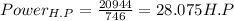Answer:
Part 1) Power required for motor = 20944 watts.
Part 2) Power required for motor in Horsepower equals = 28.075H.P
Step-by-step explanation:
Power is defined as the rate of consumption of energy. For rotational motion power is calculated as
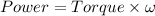
where,
 is the angular speed of the motor.
is the angular speed of the motor.
Since the rotational speed of the motor is given as 1000 rpm, the angular speed is calculated as
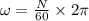
where,
'N' is the speed in rpm
Applying the given values we get
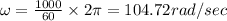
hence the power equals
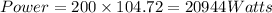
Now since we know that 1 Horse power equals 746 Watts hence 20944 Watts equals