Answer with Step-by-step explanation:
We are given that a, b, c and x are elements in the group G.
We have to find the value of x in terms of a, b and c.
a.
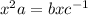
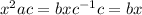
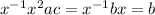 (
(
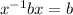 )
)
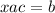
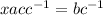
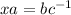 (
(
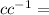 )
)
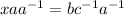
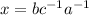
b.

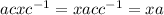 (
(
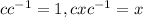 )
)
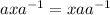 (
(
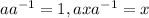 )
)

Identity equation
Hence, given equation has infinite solution and satisfied for all values of a and c.