Answer:
The answer is
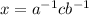 .
.
Explanation:
First, it is important to recall that the group law is not commutative in general, so we cannot assume it here. In order to solve the exercise we need to remember the axioms of group, specially the existence of the inverse element, i.e., for each element
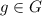 there exist another element, denoted by
there exist another element, denoted by
 such that
such that
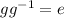 , where
, where
 stands for the identity element of G.
stands for the identity element of G.
So, given the equality
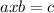 we make a left multiplication by
we make a left multiplication by
 and we obtain:
and we obtain:
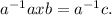
But,
 . Hence,
. Hence,
 .
.
Now, in the equality
 we make a right multiplication by
we make a right multiplication by
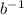 , and we obtain
, and we obtain
 .
.
Recall that
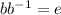 and
and
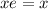 . Therefore,
. Therefore,
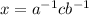 .
.