Question

A thin metal bar, insulated along its sides, is composed of five different metal connected together. The left end bar is immersed in a heat bath at 100°C and right end in a heat bath at 0°C. Starting at the left end, the pieces and lenghts are steel(2cm), brass(3cm), copper(1cm), aluminum(5cm) and silver(1cm). What is the temperature of the steel/brass interface?

Answer 1

T = 61.06 °C

Step-by-step explanation:

given data:

a thin metal bar consist of 5 different material.

thermal conductivity of ---

K {steel} = 16 Wm^{-1} k^{-1}

K brass = 125 Wm^{-1} k^{-1}

K copper = 401 Wm^{-1} k^{-1}

K aluminium =30Wm^{-1} k^{-1}

K silver = 427 Wm^{-1} k^{-1}

`(d\theta)/(dt) = (KA (T_2 -T_1))/(L)`

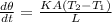
WE KNOW THAT

`(l)/(KA) = thermal\ resistance`

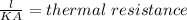
total resistance of bar = R steel + R brass + R copper + R aluminium + R silver

`R_(total) =\frac{1}[A} [(0.02)/(16) +(0.03)/(125) +(0.01)/(401) +(0.05)/(30) +(0.01)/(427)]`

`R_(total) =\frac{1}[A} * 0.00321`

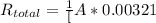
let T is the temperature at steel/brass interference

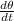`(d\theta)/(dt)` will be constant throughtout the bar

therefore we have

`(100-0)/(R_(total)) = (100-T)/(R_(steel))`

`(100-0)/(0.00321) *A = (100-T)/(0.00125) *A`

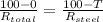
solving for T we get

T = 61.06 °C