Question

In the following ordinary annuity, the interest is compounded with each payment, and the payment is made at the end of the compounding period.

An individual retirement account, or IRA, earns tax-deferred interest and allows the owner to invest up to $5000 each year. Joe and Jill both will make IRA deposits for 30 years (from age 35 to 65) into stock mutual funds yielding 9.3%. Joe deposits $5000 once each year, while Jill has $96.15 (which is 5000/52) withheld from her weekly paycheck and deposited automatically. How much will each have at age 65? (Round your answer to the nearest cent.

Joe $

Jill $

Answer 1

Ans. Joe will have $720,862.28 and Jill will have $819,348.90 after 30 years.

Explanation:

Hi, since the interest is compounded with each payment, the effective rate of Joe is exactly equal to its compounded rate, that is 9.3%, but in the case of Jill, this rate is compounded weekly, this means that we have to divide 9.3% by 52 (which are the weeks in a year) in order to obtain an effective rate, in our case, effective weekly.

On the other hand, the time for Joe is pretty straight forward, he saves for 30 years at an effective annual interest rate of 9.3%, but Jill saves for 30*52=1560 weeks, at a rate of 0.1788% effective weekly.

They both have to use the following formula in order to find how much money will they have after 30 years of savings.

`FutureValue=(A((1+r)^(n)-1) )/(r)`

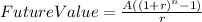
In the case of Joe, this should look like this

`FutureValue=(5,000((1+0.093)^(30)-1) )/(0.093) =720,862.28`

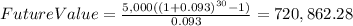
In the case of Jill, this is how this should look like.

`FutureValue=(96.15((1+0.001788)^(1560)-1) )/(0.001788) =819,348.90`

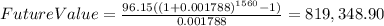
Best of luck.