Answer:
4.555 x 10^-11 m
Step-by-step explanation:
Potential difference, V = 27.3 kV
Let the wavelength is λ.
The energy associated with the potential difference, E = 27.3 keV
E = 27.3 x 1000 x 1.6 x 10^-19 J = 4.368 x 10^-15 J
The energy associated with the wavelength is given by
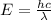
Where, h is Plank's constant = 6.63 x 10^-34 Js
c is velocity of light 3 x 10^8 m/ s
By substituting the values, we get
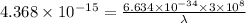
λ = 4.555 x 10^-11 m