Question

Which of the following statements do not necessarily imply that (an) is divergent? (A) (an) is eventually positive and (1/an) is null (B) (an) is unbounded (C) (an) has two convergent subsequences whose limits are not equal (D) (an) has both an increasing subsequence and a decreasing subsequence (E) All statements imply that (an) is divergent

Answer 1

D does not implies that the sequence is divergent. All others statements do.

Explanation:

Statement D: "
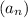`(a_n)` has both an increasing subsequence and a decreasing subsequence" does not necessarily implies that the sequence is divergent. For example, let
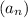`(a_n)` the sequence given by:

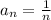`a_n=(1)/(n)` if n is odd

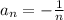`a_n=-(1)/(n)` if n is even

We can see that the subsequence
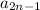`a_(2n-1)` is a decreasing sequence (the subsequence given by odd indexes). And the subsequence
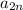`a_(2n)` is an increasing sequence (the subsequence given by even indexes).

However,
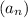`(a_n)` is a convergent sequence with limit zero.