Question

In attempting to

pass thepuck to a teammate, a hockeyplayer
gives it an initialspeedof 1.7
m/s. However, this speed is inadequate tocompensate for
the kinetic frictionbetween the puck and theice. As
a result, the puck travels only half the
distancebetweenthe players before slidingto a
halt. What minimum initial speed should the puck
havebeengiven so that it reached
theteammate, assuming that the same force of
kineticfrictionacted on the puck
everywherebetween the two players?

Answer 1

2.04 m/s

Step-by-step explanation:

Given:

• 
  `u` = initial inadequate speed of the puck = 1.7 m/s
• 
  `v` = final velocity of the puck while reaching half the distance of the targeted teammate = 0 m/s

Assumptions:

• 
  `m` = mass of the puck
• 
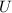  `U` = minimum initial speed of the puck so that it reaches the target
• 
  `x` = distance of the targeted teammate
• 
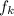  `f_k` = kinetic friction between the puck and the ice

Work-energy theorem: For the various forces acting on an object, the work done by all the forces brings a change in kinetic energy of an object which is equal to the total work done.

For the initial case, the puck travels half the distance of the target teammate. In this case, the change in kinetic energy of the puck will be equal to the work done by the friction.

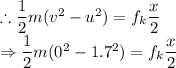`\therefore (1)/(2)m(v^2-u^2)=f_k(x)/(2)\\\Rightarrow (1)/(2)m(0^2-1.7^2)=f_k(x)/(2)`...........eqn(1)

Now, again using the work energy theorem for the puck to reach the targeted teammate, the change in kinetic energy of the puck will be equal to the work done by the kinetic friction.

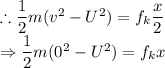`\therefore (1)/(2)m(v^2-U^2)=f_k(x)/(2)\\\Rightarrow (1)/(2)m(0^2-U^2)=f_kx`...........eqn(2)

On dividing equation (1) by (2), we have

`(-1.7^2)/(-U^2)=(1)/(2)\\\Rightarrow (1.7^2)/(U^2)=(1)/(2)\\\Rightarrow U^2= 2* 1.7^2\\\Rightarrow U^2 = 5.78\\\Rightarrow U=\pm √(5.78)\\\Rightarrow U=\pm 2.04\\\textrm{Since the speed is always positive.}\\\therefore U = 2.04\ m/s`

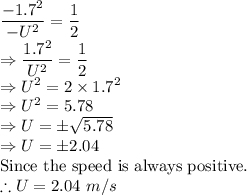
Hence, the puck must be kicked with a minimum initial speed of 2.04 m/s so that it reaches the teammate.