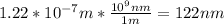Question

The so-called Lyman-α photon is the lowest energy photon in the Lyman series of hydrogen and results from an electron transitioning from the n = 2 to the n = 1 energy level. Determine the energy in eV and the wavelength in nm of a Lyman-α photon. (a) the energy in eV

(b)the wavelength in nm

Answer 1

a) 10.2 eV

b) 122 nm

Step-by-step explanation:

a) First we must obtain the energy for each of the states, which is given by the following formula:

`E_(n)=(-13.6 eV)/(n^2)`

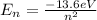
So, we have:

`E_(1)=(-13.6 eV)/(1^2)=-13.6 eV\\E_(2)=(-13.6 eV)/(2^2)=-3.4 eV`

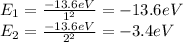
Now we find the energy that the electron loses when it falls from state 2 to state 1, this is the energy carried away by the emitted photon.

`E_(2)-E_(1)=-3.4eV-(-13.6eV)=10.2eV`

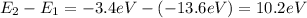
b) Using the Planck – Einstein relation, we can calculate the wavelength of the photon:

`E=h\\u`

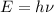
Where E is the photon energy, h the Planck constant and
`\\u` the frequency.

Recall that
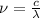`\\u=(c)/(\lambda)`, Rewriting for
`\lambda`:

`E=(hc)/(\lambda)\\\lambda=(hc)/(E)\\\lambda=((4.13*10^(-15)eV)(3*10^8(m)/(s)))/(10.2eV)=1.22*10^(-7)m`

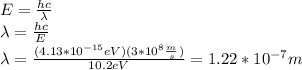
Recall that
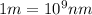`1 m=10^9nm`, So:

`1.22*10^(-7)m*(10^9nm)/(1m)=122nm`