Question

If the wavelength of an electron is 4.63 x 10^−7 m, how fast is it moving?

Answer 1

`v=1.57*10^(3)(m)/(s)`

Step-by-step explanation:

As DeBroglie equation proved by Davisson-Germer experiment says, the wavelength of an electron is related with its velocity with the equation:

λ =
`(h)/(mv)`

where m is the mass of the electron
`m=9.11*10^(-31)kg`, h is the Planck´s constant
`h=6.626*10^(-34)J.s` and v its velocity.

Solving the equation for the velocity of the electron, we have:

v = h/mλ

And replacing the values:

`v=(6.626*10^(-34)J.s)/((9.11*10^(-31)Kg)*(4.63*10^(-7)m))`

`v=1570.9(m)/(s)`

`v=1.57*10^(3)(m)/(s)`

Answer 2

it move with velocity 1571 m/s

Step-by-step explanation:

given data

wavelength λ = 4.63 ×
`10^(-7)` m

to find out

how fast is it moving

solution

we will use here de Broglie wavelength equation

that is

wavelength λ =
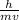`(h)/(mv)` ..........1

here h is planck constant = 6.626068 ×
`10^(-34)`

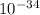
and m is mass of electron i.e = 9.10938188 ×
`10^(-31)`

and v is velocity

put all value we find velocity in equation 1

wavelength λ =
`(h)/(mv)`

v =
`(6.626068*10^(-34))/(9.10938188*10^(-31)*4.63*10^(-7))`

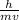
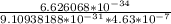
v = 1571.035464

so it move with velocity 1571 m/s