Question

Solve the following exact ordinary differential equation:

(2tz^3 + ze^(tz) - 4) dt + (3t^2z^2 + te^(tz) + 2) dz = 0

^3 = to the power of 3

Answer 1

The level curves F(t,z) = C for any constant C in the real numbers

where

`F(t,z)=z^3t^2+e^(tz)-4t+2z`

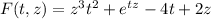
Explanation:

Let's call

`M(t,z)=2tz^3+ze^(tz)-4`

`N(t,z)=3t^2z^2+te^(tz)+2`

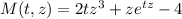
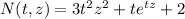
Then our differential equation can be written in the form

1) M(t,z)dt+N(t,z)dz = 0

To see that is an exact differential equation, we have to show that

2)
`(\partial M)/(\partial z)=(\partial N)/(\partial t)`

But

`(\partial M)/(\partial z)=(\partial (2tz^3+ze^(tz)-4))/(\partial z)=6tz^2+e^(tz)+zte^(tz)`

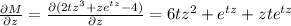
In this case we are considering t as a constant.

Similarly, now considering z as a constant, we obtain

`(\partial N)/(\partial t)=(\partial (3t^2z^2+te^(tz)+2))/(\partial t)=6tz^2+e^(tz)+zte^(tz)`

So, equation 2) holds and then, the differential equation 1) is exact.

Now, we know that there exists a function F(t,z) such that

3)
`(\partial F)/(\partial t)=M(t,z)`

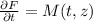
AND

4)
`(\partial F)/(\partial z)=N(t,z)`

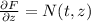
We have then,

`(\partial F)/(\partial t)=2tz^3+ze^(tz)-4`

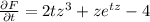
Integrating on both sides

`F(t,z)=\int (2tz^3+ze^(tz)-4)dt=2z^3\int tdt+z\int e^(tz)dt-4\int dt+g(z)`

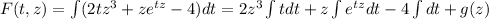
where g(z) is a function that does not depend on t

so,

`F(t,z)=(2z^3t^2)/(2)+z(e^(tz))/(z)-4t+g(z)=z^3t^2+e^(tz)-4t+g(z)`

Taking the derivative of F with respect to z, we get

`(\partial F)/(\partial z)=3z^2t^2+te^(tz)+g'(z)`

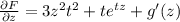
Using equation 4)

`3z^2t^2+te^(tz)+g'(z)=3z^2t^2+te^(tz)+2`

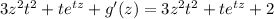
Hence

`g'(z)=2\Rightarrow g(z)=2z`

The function F(t,z) we were looking for is then

`F(t,z)=z^3t^2+e^(tz)-4t+2z`

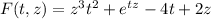
The level curves of this function F and not the function F itself (which is a surface in the space) represent the solutions of the equation 1) given in an implicit form.

That is to say,

The solutions of equation 1) are the curves F(t,z) = C for any constant C in the real numbers.

Attached, there are represented several solutions (for c = 1, 5 and 10)