Question

A ferry leaves Nanaimo to make the 22 km trip to Vancouver at the same time as a forry leaves Vancouver for Nanaimo. The ferry leaving Nanaimo travels 2 km/h faster than the other ferry How far are they from Vancouver when they meet 45 minutes later?

Answer 1

They are 11.7475km away from Vancouver when they meet.

Explanation:

The first step to solve this problem is modeling the position of each ferry. The position can be modeled by a first order equation in the following format:

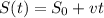`S(t) = S_(0) + vt`, in which
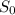`S_(0)` is the initial position of the ferry, t is the time in hours and v is the speed in km/h.

I am going to say that the positive direction is from Nanaimo to Vancouver, and that Nanaimo is the position 0 and Vancouver the position 22.

First ferry:

Leaves Nanaimo, so
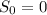`S_(0) = 0`. It is 2km/h faster than the second ferry, so i am going to say that
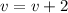`v = v + 2`. It moves in the positive direction, so v is positive. The equation of the position of this train is modeled as:

`S_(1)(t) = 0 + (v+2)t`,

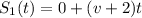Second ferry:

Leaves Vancouver, so
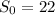`S_(0) = 22`. It has a speed of v, that is negative, since it moves in the negative direction. So

`S_(2)(t) = 22 - vt`

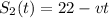
The problem states that they meet in 45 minutes. Here we have to pay attention. Since the speed is in km/h, the time needs to be in h. So 45 minutes = 0.75h.

They meet in 0.75h. It means that

`S_(1)(0.75) = S_(2)(0.75)`

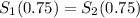
With this we find the value o v, and replace in the equation of
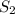`S_(2)` to see how far they are from Vancouver when they meet.

`S_(1)(0.75) = S_(2)(0.75)`

`0.75(v+2) = 22 - 0.75v`

`0.75v + 1.50 = 22 - 0.75v`

`1.50v = 20.50`

`v = (20.50)/(1.50)`

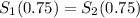
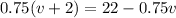
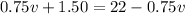
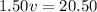
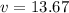`v = 13.67`km/h.

`S_(2)(t) = 22 - vt`

`S_(2)(0.75) = 22 - 13.67*0.75 = 11.7475`

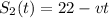
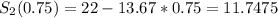
They are 11.7475km away from Vancouver when they meet.