Question

kindly solve using the second shifting theorem. thanks. please include explanation that I can understand. many thanks. L[t^2 u(t – 3)] -3)]

Answer 1

`(2)/(s^3)e^(-3s)\ +\ (6)/(s^2)e^(-3s)\ +\ (9)/(s)e^(-3s)\ -\ (3)/(s)`

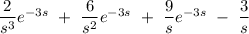
Explanation:

Given polynomial,

`f(t)\ =\ t^2.u(t-3)\ -\ 3`

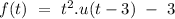
we can write above polynomial as

`f(t)\ =\ (t-3+3)^2.u(t-3)\ -\ 3`

`=\ ((t-3)^2\ +\ 2* 3* (t-3)\ +\ 3^2).u(t-3)-3`

`=\ (t-3)^2.u(t-3)\ +\ 6(t-3).u(t-3)\ +\ 9.u(t-3)\ -\ 3`

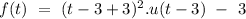
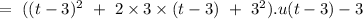
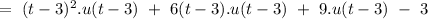
Now, we have to calculate the Laplace of above polynomial

according to shifting property of Laplace transform, we can write

`f(t-t_0)\ =\ F(s).e^(-st_0)`

So, we can write the Laplace transform of above polynomial as

`L[f(t)]\ =\ L[(t-3)^2.u(t-3)\ +\ 6(t-3).u(t-3)\ +\ 9.u(t-3)\ -\ 3]`

`=\ (2)/(s^3)e^(-3s)\ +\ (6)/(s^2)e^(-3s)\ +\ (9)/(s)e^(-3s)\ -\ (3)/(s)`

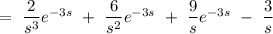
So, the Laplace transform of the given polynomial will be
`\ (2)/(s^3)e^(-3s)\ +\ (6)/(s^2)e^(-3s)\ +\ (9)/(s)e^(-3s)\ -\ (3)/(s)`