Answer:
If the intersection is finite the statement is true, but if the intersection is infinite the statement is false.
Explanation:
From the statement of the problem I am not sure if the intersection is finite or infinite. Then, I will study both cases.
Let us consider first the finite case:
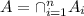 . Because the condition A1 ⊇ A2 ⊇ A3 ⊇ A4 ... we can deduce that the set
. Because the condition A1 ⊇ A2 ⊇ A3 ⊇ A4 ... we can deduce that the set
 is a subset of each set
is a subset of each set
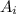 with
with
 . Thus,
. Thus,
 .
.
Therefore, as
 is infinite, the intersection is infinite.
is infinite, the intersection is infinite.
Now, if we consider the infinite intersection, i.e.
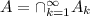 the reasoning is slightly different. Take the sets
the reasoning is slightly different. Take the sets
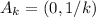 (this is, the open interval between 0 and
(this is, the open interval between 0 and
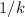 .)
.)
Notice that (0,1) ⊇ (0,1/2) ⊇ (0, 1/3) ⊇(0,1/4) ⊇...So, the hypothesis of the problem are fulfilled. But,

In order to prove the above statement, choose a real number
 between 0 and 1. Notice that, no matter how small
between 0 and 1. Notice that, no matter how small
 is, there is a natural number
is, there is a natural number
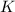 such that
such that
 . Then, the number
. Then, the number
 is not in any interval
is not in any interval
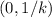 with
with
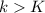 . Therefore,
. Therefore,
 is not in the set [tex]\cap_{k=1}^{\infty}(0,1/k)[\tex].
is not in the set [tex]\cap_{k=1}^{\infty}(0,1/k)[\tex].