Answer:
Approximate linear dimension is 2 light years.
Step-by-step explanation:
Radius of the spiral galaxy r = 62000 LY
Thickness of the galaxy h = 700 LY
Volume of the galaxy = πr²h
= (3.14)(62000)²(700)
= (3.14)(62)²(7)(10)⁸
= 84568×10⁸
=
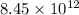 (LY)³
(LY)³
Since galaxy contains number of stars = 1078 billion stars ≈

Now volume covered by each star of the galaxy =
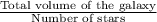
=
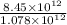
= 7.839 Light Years
Now the linear dimension across the volume
=

=

= 1.99 LY
≈ 2 Light Years
Therefore, approximate linear dimension is 2 light years.