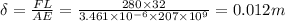Question

Consider a cylindrical nickel wire 2.1 mm in diameter and 3.2 × 104 mm long. Calculate its elongation when a load of 280 N is applied. Assume that the deformation is totally elastic and that the elastic modulus for nickel is 207 GPa (or 207 × 109 N/m2).

Answer 1

Total elongation will be 0.012 m

Step-by-step explanation:

We have given diameter of the cylinder = 2.1 mm

Length of wire
`L=3.2* 10^4mm`

So radius
`r=(d)/(2)=(2.1)/(2)=1.05mm=1.05* 10^(-3)m`

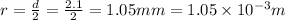
Load F = 280 N

Elastic modulus = 207 Gpa

Area of cross section
`A=\pi r^2=3.14* (1.05* 10^(-3))^2=3.461* 10^(-6)m^2`

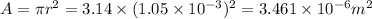
We know that elongation in wire is given by
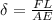`\delta =(FL)/(AE)`, here F is load, L is length, A is area and E is elastic modulus

So
`\delta =(FL)/(AE)=(280* 32)/(3.461* 10^(-6)* 207* 10^9)=0.012m`