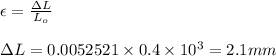Question

A round steel bar, 0.02 m in diameter and 0.40 m long, is subjected to a tensile force of 33,000 kg. Y=E= 2E10 kg/m^2. (modulus).Calculate the elongation in meters.

Answer 1

The elongation in the bar equals 2.1 millimeters.

Step-by-step explanation:

We know from Hooke's Law

`\sigma =E* \epsilon`

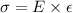
Where

`\sigma` is stress in the material

`\epsilon` is strain in the material

'E' is the young's modulus of the material

Now we know that

`stress =(Force)/(Area)`

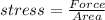
Applying values we get

`\sigma =(33000)/((\pi )/(4)* (0.02)^(2))=105.042* 10^(6)kg/m^(2)`

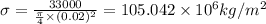
Applying the values in the Hooke's relation we obtain

`\epsilon =(\sigma )/(E)\\\\\epsilon =(105.042* 10^(6))/(2* 10^(10))=0.0052521`

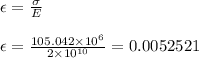
Now by definition of strain we have

`\epsilon =(\Delta L)/(L_(o))\\\\\Delta L=0.0052521* 0.4* 10^(3)=2.1mm`