Question

Consider a nuclear power plant that produces 1200 MW of power and has a conversion efficiency of 34 percent (that is, for each unit of fuel energy used, the plant produces 0.34 units of electrical energy. Assuming continuous operation, determine the amount of nuclear fuel consumed by the plant per year.

Answer 1

Answer with Explanation:

The relation between power and energy is

`Energy=Power* Time`

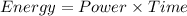
Since the nuclear reactor operates at 1200 MW throughout the year thus the energy produced in 1 year equals

`E=1200* 10^(6)* 3600* 24* 365=3.784* 10^(16)`

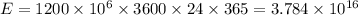
Now from the energy mass equivalence we have

`E=mass* c^2`

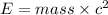
where

'c' is the speed of light in free space

Thus equating both the above values we get

`3.784* 10^(16)=mass* (3* 10^(8))^(2)\\\\\therefore mass=(3.784* 10^(16))/(9* 10^(16))=0.42kg`

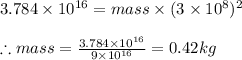
Since it is given that 1 kg of mass is 34% effective thus the mass reuired for the reactor is

`mass_(req)=(mass)/(\eta )=(0.43)/(0.34)=1.235`

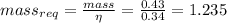
Thus 1.235 kg of nuclear fuel is reuired for operation.