Question

Find an equation of a line with the x- and y-intercepts below. Use exact fractions when necessary.

x-intercept 7; y-intercept -5

Answer 1

The line with the x- and y-intercepts below has the following equation:

`f(x) = (5x)/(7) - 5`

Explanation:

The equation of the line has the following format:

`f(x) = ax + b`

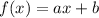
We are given two points, we are going to substitute them into the above equation, and find the equation of the line given the conditions.

Solution

Starting from the y-intercept makes the solution easier, since the term a is multiplied by 0

y-intercept -5

This means that when
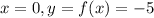`x = 0, y = f(x) = -5`, so:

`f(x) = ax + b`

`-5 = a(0) + b`

`b = -5`

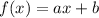
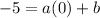
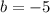
For now, the line has the following equation:

`f(x) = ax - 5`

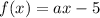
x-intercept 7

This means that when
`y = f(x) = 0,x = 7`, so:

`f(x) = ax - 5`

`0 = 7(a) - 5`

`7a = 5`

`a = (5)/(7)`

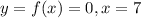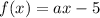
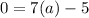
So, the line with the x- and y-intercepts below has the following equation:

`f(x) = (5x)/(7) - 5`