Answer:
Explanation:
Given that *is the binary operation in the sets of integers.
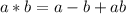
closure: a-b+ab is again an integer belongs to Z. Hence closure is true.
Associativity:
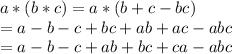
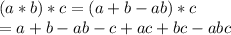
The two are not equal. Hence this cannot be a group as associtiavity does not hold good.