Question

Use Gaussian Elimination to find an equation of a polynomial that passes through points A(-5,-3), B(-2,3). C(3,3), D(6,19). Indicates row operations with the R notation. Leave coefficients in fraction form, do not report in decimals.

Answer 1

The polynomial equation that passes through the points is
`2-(2)/(3)x+(1)/(12)x^(2)+(1)/(12)x^(3)`

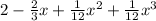
Explanation:

Suppose you have a function y = f(x) which goes through these points

A(-5,-3), B(-2,3). C(3,3), D(6,19)

there is a polynomial P(x) of degree 3 which goes through these point.

We use the fact that four distinct points will determine a cubic function.

P(x) is the degree 3 polynomial through the 4 points, a standard way to write it is

`P(x) = a+bx+cx^2+dx^3`

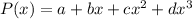
Next replace the given points one by one, which leads to a system of 4 equations and 4 variables (namely a,b,c,d)

`-3=a+b\cdot-5+c\cdot -5^2+d\cdot -5^3\\3=a+b\cdot-2+c\cdot -2^2+d\cdot -2^3\\3=a+b\cdot 3+c\cdot 3^2+d\cdot 3^3\\19=a+b\cdot 6+c\cdot 6^2+d\cdot 6^3`

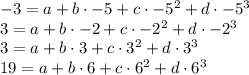
We can rewrite this system as follows:

`-3=a-5\cdot b+25\cdot c-125\cdot d\\3=a-2\cdot b+4\cdot c-8\cdot d\\3=a+3\cdot b+9\cdot c+27\cdot d\\19=a+6\cdot b+36\cdot c+216\cdot d`

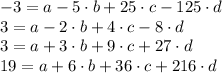
To use the Gaussian Elimination we need to express the system of linear equations in matrix form (the matrix equation Ax=b).

The coefficient matrix (A) for the above system is

`\left[\begin{array}{cccc}1&-5&25&-125\\1&-2&4&-8\\1&3&9&27\\1&6&36&216\end{array}\right]`

the variable matrix (x) is

`\left[\begin{array}{c}a&b&c&d\end{array}\right]`

and the constant matrix (b) is

`\left[\begin{array}{c}-3&3&3&19\end{array}\right]`

We also need the augmented matrix, it is obtained by appending the columns of the coefficient matrix and the constant matrix.

`\left[\begin{array}c1&-5&25&-125&-3\\1&-2&4&-8&3\\1&3&9&27&3\\1&6&36&216&19\end{array}\right]`

To transform the augmented matrix to the reduced row echelon form we need to follow these steps:

• Subtract row 1 from row 2
  `\left(R_2=R_2-R_1\right)`

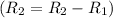
`\left[\begin{array}c1&-5&25&-125&-3\\0&3&-21&117&6\\1&3&9&27&3\\1&6&36&216&19\end{array}\right]`

• Subtract row 1 from row 3
  `\left(R_3=R_3-R_1\right)`

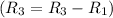
`\left[\begin{array}cccc1&-5&25&-125&-3\\0&3&-21&117&6\\0&8&-16&152&6\\1&6&36&216&19\end{array}\right]`

• Subtract row 1 from row 4
  `\left(R_4=R_4-R_1\right)`

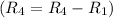
`\left[\begin{array}c1&-5&25&-125&-3\\0&3&-21&117&6\\0&8&-16&152&6\\0&11&11&341&22\end{array}\right]`

• Divide row 2 by 3
  `\left(R_2=(R_2)/(3)\right)`

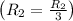
`\left[\begin{array}c1&-5&25&-125&-3\\0&1&-7&39&2\\0&8&-16&152&6\\0&11&11&341&22\end{array}\right]`

• Add row 2 multiplied by 5 to row 1
  `\left(R_1=R_1+\left(5\right)R_2\right)`

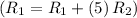
`\left[\begin{array}c1&0&-10&-70&7\\0&1&-7&39&2\\0&8&-16&152&6\\0&11&11&341&22\end{array}\right]`

• Subtract row 2 multiplied by 8 from row 3
  `\left(R_3=R_3-\left(8\right)R_2\right)`

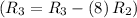
`\left[\begin{array}cccc1&0&-10&-70&7\\0&1&-7&39&2\\0&0&40&-160&-10\\0&11&11&341&22\end{array}\right]`

• Subtract row 2 multiplied by 11 from row 4
  `\left(R_4=R_4-\left(11\right)R_2\right)`

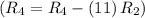
`\left[\begin{array}c1&0&-10&-70&7\\0&1&-7&39&2\\0&0&40&-160&-10\\0&0&88&-88&0\end{array}\right]`

• Divide row 3 by 40
  `\left(R_3=(R_3)/(40)\right)`

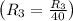
`\left[\begin{array}cccc1&0&-10&-70&7\\0&1&-7&39&2\\0&0&1&-4&-1/4\\0&0&88&-88&0\end{array}\right]`

• Add row 3 multiplied by 10 to row 1
  `\left(R_1=R_1+\left(10\right)R_3\right)`

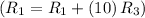
`\left[\begin{array}cccc1&0&0&30&9/2\\0&1&-7&39&2\\0&0&1&-4&-1/4\\0&0&88&-88&0\end{array}\right]`

• Add row 3 multiplied by 7 to row 2
  `\left(R_2=R_2+\left(7\right)R_3\right)`

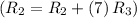
`\left[\begin{array}cccc1&0&0&30&9/2\\0&1&0&11&1/4\\0&0&1&-4&-1/4\\0&0&88&-88&0\end{array}\right]`

• Subtract row 3 multiplied by 88 from row 4
  `\left(R_4=R_4-\left(88\right)R_3\right)`

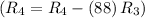
`\left[\begin{array}c1&0&0&30&9/2\\0&1&0&11&1/4\\0&0&1&-4&-1/4\\0&0&0&264&22\end{array}\right]`

• Divide row 4 by 264
  `\left(R_4=(R_4)/(264)\right)`

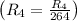
`\left[\begin{array}cccc1&0&0&30&9/2\\0&1&0&11&1/4\\0&0&1&-4&-1/4\\0&0&0&1&1/12\end{array}\right]`

• Subtract row 4 multiplied by 30 from row 1
  `\left(R_1=R_1-\left(30\right)R_4\right)`

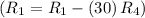
`\left[\begin{array}c1&0&0&0&2\\0&1&0&11&1/4\\0&0&1&-4&-1/4\\0&0&0&1&1/12\end{array}\right]`

• Subtract row 4 multiplied by 11 from row 2
  `\left(R_2=R_2-\left(11\right)R_4\right)`

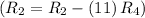
`\left[\begin{array}c1&0&0&0&2\\0&1&0&0&-2/3\\0&0&1&-4&-1/4\\0&0&0&1&1/12\end{array}\right]`

• Add row 4 multiplied by 4 to row 3
  `\left(R_3=R_3+\left(4\right)R_4\right)`

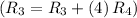
`\left[\begin{array}c1&0&0&0&2\\0&1&0&0&-2/3\\0&0&1&0&1/12\\0&0&0&1&1/12\end{array}\right]`

From the reduced row-echelon form the solutions are:

`\left[\begin{array}{c}a=2&b=-2/3&c=1/12&d=1/12\end{array}\right]`

The polynomial P(x) is:

`2-(2)/(3)x+(1)/(12)x^(2)+(1)/(12)x^(3)`

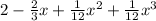
We can check our solution plotting the polynomial and checking that it passes through the points.