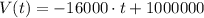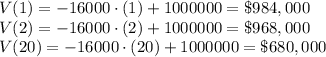Question

A new building that costs $1,000,000 has a useful life of 25 years and a scrap value of $600,000. Using straight-line depreciation, find the equation for the value V in terms of t, where t is in years. (Make sure you use t and not x in your answer.)

V(t) =



Find the value after 1 year, after 2 years, and after 20 years.

Value after 1 year $
Value after 2 years $
Value after 20 years $

Answer 1

The equations for the value V in terms of t is
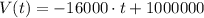`V(t)=-16000\cdot t+1000000` and the value of the building

after 1 year is $984,000

after 2 years is $968,000

after 20 years is $680,000

Explanation:

With the straight-line depreciation method, the value of an asset is reduced uniformly over each period until it reaches its salvage value(It is the value of the asset at the end of its useful life).

We know from the information given the year = 0 the building costs $1,000,000 and a the year = 25 it costs $600,000.

With this information, you can calculate the decrease in value of the building due to age. We use the slope of a line formula because is a straight-line depreciation.

If (0, $1,000,000) is the first point and (25, $600,000) is the second point. we have

`m=(V_(2) -V_(1))/(t_(2)-t_(1)) =(600000-1000000)/(25-0) =-16000 (\$)/(years)`

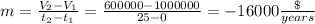
To find the equation for the value V in terms of t, we use the point-slope form, this expression let you calculate the value of the building at the end of the year (t)

`V-V_(0)= m(t- t_(0))\\V-1000000=-16000(x-0)\\V=-16000\cdot t+1000000`

To find the value after 1 year, after 2 years, and after 20 years. We put the year into the equation
`V(t)=-16000\cdot t+1000000`

`V(1)=-16000\cdot (1)+1000000=\$984,000\\V(2)=-16000\cdot (2)+1000000=\$968,000\\V(20)=-16000\cdot (20)+1000000=\$680,000`