Answer:
Explanation:
a) We want to prove that
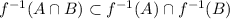 . Then, we can do that proving that every element of
. Then, we can do that proving that every element of
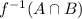 is an element of
is an element of
 too.
too.
Then, suppose that
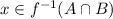 . From the definition of inverse image we know that
. From the definition of inverse image we know that
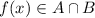 , which is equivalent to
, which is equivalent to
 and
and
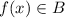 . But, as
. But, as
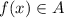 we can affirm that
we can affirm that
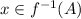 and, because
and, because
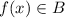 we have
we have
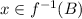 .
.
Therefore,
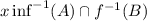 .
.
b) We want to prove that
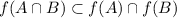 . Here we will follow the same strategy of the above exercise.
. Here we will follow the same strategy of the above exercise.
Assume that
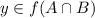 . Then, there exists
. Then, there exists
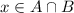 such that
such that
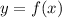 . But, as
. But, as
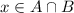 we know that
we know that
 and
and
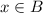 . From this, we deduce
. From this, we deduce
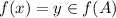 and
and
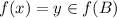 . Therefore,
. Therefore,
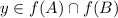 .
.
c) Consider the constant function
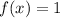 for every real number
for every real number
 . Take the sets
. Take the sets
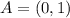 and
and
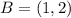 .
.
Notice that
 =Ø, so
=Ø, so
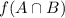 =Ø. But
=Ø. But
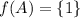 and
and
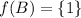 , so
, so
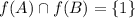 .
.