Answer:
False.
Step-by-step explanation:
From Kepler's Third Law of plenetary motion, we know that:
"The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit."
Or, as expressed in mathematical terms:
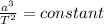 , where a is the semi-major axis of the orbit (the distance from the center), and T is the orbital period of the satellite.
, where a is the semi-major axis of the orbit (the distance from the center), and T is the orbital period of the satellite.
From this expression we can clearly see that if the orbit's semi-major axis is doubled, orbital period will be
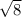 times longer to compensate the variation.
times longer to compensate the variation.