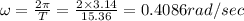Question

If a pendulum is 10m long, (a) what is the natural frequency and the period of vibration on the earth, where the free-fall acceleration is 9.81 m/s^2 and (b) what is the natural frequency and the period of vibration on the moon, where the free-fall acceleration is 1.67 m/s^2?

Answer 1

(a) Natural frequency = 0.99 rad/sec (b) 0.4086 rad/sec

Step-by-step explanation:

We have given length of pendulum = 10 m

(a) Acceleration due to gravity
`=9.81m/sec^2`

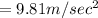
Time period of pendulum is given by
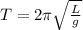`T=2\pi\sqrt{(L)/(g)}`, L is length of pendulum and g is acceleration due to gravity

So
`T=2\pi\sqrt{(L)/(g)}=2* 3.14* \sqrt{(10)/(9.81)}=6.34sec`

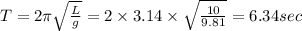
Natural frequency is given by
`\omega =(2\pi )/(T)=(2* 3.14)/(6.34)=0.99rad/sec`

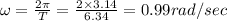
(b) In this case acceleration due to gravity
`g=1.67m/sec^2`

So time period
`T=2\pi\sqrt{(L)/(g)}=2* 3.14* \sqrt{(10)/(1.67)}=15.3674sec\`

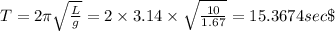
Natural frequency
`\omega =(2\pi )/(T)=(2* 3.14)/(15.36)=0.4086rad/sec`