Question

Determine the stopping distances for a car with an initial speed of 88 km/h and human reaction time of 2.0 s for the following accelerations. (a) a = -4.0 m/s^2 (b) a = -8.0 m/s^2

Answer 1

Step-by-step explanation:

Given that,

Initial speed of the car, u = 88 km/h = 24.44 m/s

Reaction time, t = 2 s

Distance covered during this time,
`d=24.44* 2=48.88\ m`

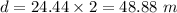
(a) Acceleration,
`a=-4\ m/s^2`

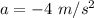
We need to find the stopping distance, v = 0. It can be calculated using the third equation of motion as :

`s=(v^2-u^2)/(2a)`

`s=(-(24.44)^2)/(2* -4)`

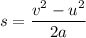
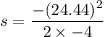
s = 74.66 meters

s = 74.66 + 48.88 = 123.54 meters

(b) Acceleration,
`a=-8\ m/s^2`

`s=(v^2-u^2)/(2a)`

`s=(-(24.44)^2)/(2* -8)`

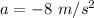
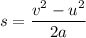
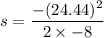
s = 37.33 meters

s = 37.33 + 48.88 = 86.21 meters

Hence, this is the required solution.