Question

A car has mass 1500 kg and is traveling at a speed of 35 miles/hour. what is its kinetic energy in joules? (Be sure to convert miles/hour to m/s). If the car increases its speed to 70 miles/hour, by what factor does its kinetic energy increase? show work

Answer 1

The kinetic energy of car with mass 1500 kg and with speed of 35 miles/hour is KE=183598 J and when the car increases its speed to 70 miles/hour the kinetic energy changes by a factor of 4.

Explanation:

The first step is to convert the speed miles/hour to m/s.

`35(miles)/(hour) *(1609.34 \>m)/(1 \>miles)*(1 \>hour)/(3600 \> s)=15.646 (m)/(s)`

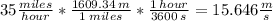
Next, the formula for the kinetic energy is

`KE=(1)/(2) mv^(2)`

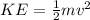
So input the values given:

`KE=(1)/(2) (1500)(15.646)^(2)\\KE=750 \cdot (15.646)^(2)\\KE=183597.987 = 183598 (kg \cdot \>m^(2))/(s^(2)) \\KE=183598 \>J`

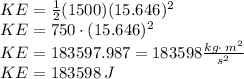
Notice that the speed of 70 miles/hour is the double of 35 miles/hour so we can say that
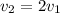`v_(2)=2v_(1)` and use the formula for the kinetic energy

`KE_(2) =(1)/(2) m(v_(2)) ^(2)\\if \: v_(2)= 2v_(1), then \:\\KE_(2) =(1)/(2) m(2v_(1)) ^(2)\\KE_(2) =(1)/(2) m4(v_(1))^(2)\\KE_(2) =4((1)/(2) m(v_(1))^(2))\\We \:know \:that \:KE_(1) =(1)/(2) m(v_(1))^(2) so\\KE_(2) =4(KE_(1))`

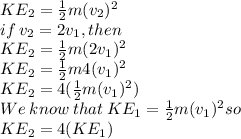
We can see that when the car increases its speed to 70 miles/hour the kinetic energy changes by a factor of 4.