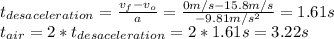Question

A ball is kicked with an initial velocity of 18.1 m/s in the horizontal direction and 15.8 m/s in the vertical direction. For how long does the ball remain in the air?

Answer 1

3.22 s

Step-by-step explanation:

The ball would describe a projectile motion, where the horizontal velocity will remain constant, as there are no forces that act on the x-axis, and the vertical velocity will vary because of gravity in the following way:

1. First, the ball will go up, but the vertical velocity will decrease until it has a value of 0.

2. After the vertical velocity has reached the value of 0, the ball will start to fall, with the vertical velocity increasing because of gravity.

You need to know that the time that the ball's verical velocity takes to reach 0 is exactly the same that it takes to go from 0 to its original vertical velocity:

`a = (v_f - v_o)/(t)\\t = (v_f - v_o)/(a)`

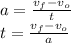
And not only the time will be the same, but also the distance traveled. Therefore, we can conclude that the time that the ball remain in the air is simply two times the time it takes for the ball to desacelerate:

`t_(desaceleration) = (v_f - v_o)/(a) = (0m/s - 15.8m/s)/(-9.81 m/s^2) =1.61 s\\t_(air) = 2* t_(desaceleration) = 2*1.61s = 3.22 s`