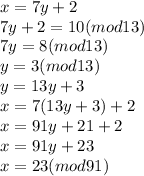Question

Arithmetic Modular Composite Numbers (4 marks). Carry out the following calcula- tions by hand by using the Chinese Remainder Theorem to split each operation into two operations modulo smaller numbers. You must show your work to receive full credit (a) 23 x 36 mod 55 (b) 29 x 51 mod 91

Answer 1

a) 23 x 36 (mod 55) = 3 (mod 55)

b) 23 x 36 (mod 55) = 23 (mod 91)

Explanation:

The Chinese Remainder Theorem lets us split a composite modulo into its prime components and solve for smaller numbers.

a) Using the Chinese Remainder Theorem, we have that 55 = 11 x 5

Since 11 and 5 are relatively prime numbers, we can use the Theorem and rewrite 23 x 36 mod 55 as: 23 x 36 (mod 11) and 23 x 36 (mod 5).

First we will work with 23 x 36 (mod 11)

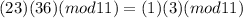`(23)(36)(mod 11) = (1)(3) (mod 11)` (Since 23 is congruent to 1 modulo 11 and 36 is congruent to 3 modulo 11)

Now we do the same with 23 x 36 (mod 5)

`(23)(36) (mod 5) = (3)(1) (mod5) = 3 (mod 5)`

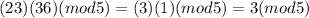
Now we will use the Chinese Remainder Theorem to solve this pair of equations:

x = 3 (mod 11) and x = 3(mod 5)

`x=5y+3\\5y+3=3(mod 11)\\5y=0(mod 11)\\y=0 (mod 11)\\y=11z\\x=5(11z)+3\\x=55z + 3\\x=3(mod 55)\\`

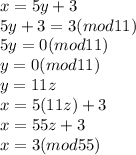
b) We are going to use the same procedure from a)

91 = 13 x 7

29 x 51 (mod 91) = 29 x 51 (mod 13) and 29 x 51 (mod 7)

29 x 51 (mod 13) = 3 x 12 (mod 13) = 36 (mod 13) = 10 (mod 13)

29 x 51 (mod 7) = 1 x 2 (mod 7) = 2 (mod 7)

Our pair of equations is x = 10 (mod 13) and x = 2 (mod 7)

`x= 7y + 2\\7y + 2 = 10(mod13)\\7y= 8(mod13)\\y= 3 (mod 13)\\y=13y+3\\x=7(13y+3) + 2\\x=91y +21+2\\x=91y+23\\x= 23 (mod 91)`