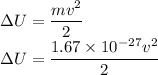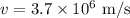Question

Two 2.3 cm -diameter disks face each other, 2.9 mm apart. They are charged to ±16nC . A) What is the electric field strength between the disks?

Express your answer to two significant figures and include the appropriate units.

B) A proton is shot from the negative disk toward the positive disk. What launch speed must the proton have to just barely reach the positive disk?
Express your answer to two significant figures and include the appropriate units.

Answer 1

A)
`391*10^4\ \rm N/C`

B
`3.7*10^6\ \rm m/s`

Step-by-step explanation:

Given:

• Diameter of each disc , d=2.3 cm
• Magnitude of total Charge on each disc Q=16 nC

A)Let
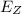`E_Z` Electric Field due to a disc of Radius R containing charge Q at a distance Z from its centre in direction perpendicular to the plane of the disc given by

since the disks are identical and charges on them are same and and distance of point from their centres are also same so the Electric field at P will be twice the Electric Field due to one.

`E_z=(4kQ)/(R^2)\ \left (1-(z)/(√(R^2+z^2)) \right`)\\\\
`E_z=(4*9*10^9*16*10^(-9))/(0.015^2)\ \left (1-(0.00145)/(√(0.015^2+0.00145^2)) \right )\\\\E_z=391*10^4\ \rm N/C`

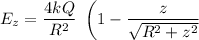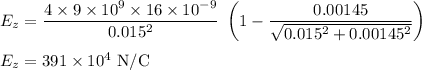
The Direction of Electric Field will be from disk containing positive charge towards negative charge.

B))Let
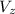`V_z` Electric potential due to a disc of Radius R containing charge Q at a distance Z from its centre in direction perpendicular to the plane of the disc given by
`V_z=(2kQ)/(R^2)`

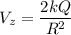
At the centre of both the disks z=0

`\left ({√(R^2+0^2)} -0 \right )\\\\V_z=(2kQ)/(R)\\V-z=19200\ V`

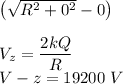
At z=0.0029 m

`V_z=(2kQ)/(R^2)\ \left (√(R^2+z^2)}-z}{ \right )\\\\V_z=(2*9*10^9*16*10^(-9))/(0.015^2)\ \left (√(0.015^2+0.0029^2)}-0.0029}{ \right )\\\\V_z=15360\ \rm V`

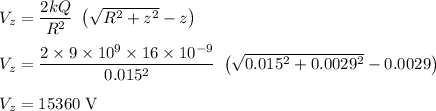
since the disks are identical and charges on them are same and and distance of point from their centres are also same so the Electric potential at P will be twice the Electric Field due to one.

So the change in Electric potential is

`\Delta V=2(19200+15360)\\\\\Delta V=69120\ \rm V`

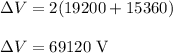
Change in potential Energy is

`\Delta U=\Delta V* e\\`

`\Delta U=1.15*10^(-14)\ \rm J`

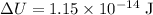
The change in potential Energy will be equal to the the change in kinetic Energy of the proton

`\Delta U=(mv^2)/(2)\\\Delta U=(1.67*10^(-27)v^2)/(2)\\`

`v=3.7*10^(6)\ \rm m/s`