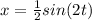Question

Write down the explicit solution for each of the following: a) x’=t–sin(t); x(0)=1

b) x’+2x=4; x(0)=5
c) x’’+4x=0; x(0)=0; x’(0)=1

Answer 1

a) x=(t^2)/2+cos(t), b) x=2+3e^(-2t), c) x=(1/2)sin(2t)

Explanation:

Let's solve by separating variables:

`x'=(dx)/(dt)`

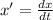
a) x’=t–sin(t), x(0)=1

`dx=(t-sint)dt`

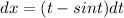
Apply integral both sides:

`\int {} \, dx=\int {(t-sint)} \, dt\\\\x=(t^2)/(2)+cost +k`

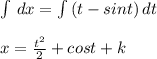
where k is a constant due to integration. With x(0)=1, substitute:

`1=0+cos0+k\\\\1=1+k\\k=0`

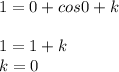
Finally:

`x=(t^2)/(2) +cos(t)`

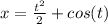
b) x’+2x=4; x(0)=5

`dx=(4-2x)dt\\\\(dx)/(4-2x)=dt \\\\\int {(dx)/(4-2x)}= \int {dt}\\`

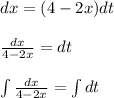
Completing the integral:

`-(1)/(2) \int{((-2)dx)/(4-2x)}= \int {dt}`

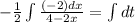
Solving the operator:

`-(1)/(2)ln(4-2x)=t+k`

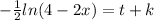
Using algebra, it becomes explicit:

`x=2+ke^(-2t)`

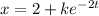
With x(0)=5, substitute:

`5=2+ke^(-2(0))=2+k(1)\\\\k=3`

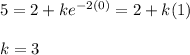
Finally:

`x=2+3e^(-2t)`

c) x’’+4x=0; x(0)=0; x’(0)=1

Let
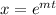`x=e^(mt)` be the solution for the equation, then:

`x'=me^(mt)\\x''=m^(2)e^(mt)`

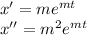
Substituting these equations in c)

`m^(2)e^(mt)+4(e^(mt))=0\\\\m^(2)+4=0\\\\m^(2)=-4\\\\m=2i`

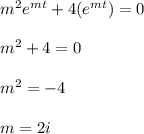
This becomes the solution m=α±βi where α=0 and β=2

`x=e^(\alpha t)[Asin\beta t+Bcos\beta t]\\\\x=e^(0)[Asin((2)t)+Bcos((2)t)]\\\\x=Asin((2)t)+Bcos((2)t)`

Where A and B are constants. With x(0)=0; x’(0)=1:

`x=Asin(2t)+Bcos(2t)\\\\x'=2Acos(2t)-2Bsin(2t)\\\\0=Asin(2(0))+Bcos(2(0))\\\\0=0+B(1)\\\\B=0\\\\1=2Acos(2(0))\\\\1=2A\\\\A=(1)/(2)`

Finally:

`x=(1)/(2) sin(2t)`