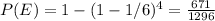Answer:
The probability that at least one 5 will appear in 4 rolls of die equals

Step-by-step explanation:
The given question can be solved by Bernoulli's trails which states that
If probablity of success of an event is 'p' then the probability that the event occurs at least once in 'n' successive trails equals
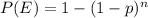
Since in our case the probability of getting 5 on roll of a die equals 1/6 thus we have p = 1/6
Applying the values in the given equation the probability of success in 4 rolls of die is thus given by