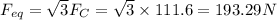Question

Three equal charges are placed at the corners of an equilateral triangle 0.50 m on a side. What are the magnitude of the force on each charge if the charges are each -3.1 x 10^-9 C?

Answer 1

the magnitude of the force is 192.29 N

Solution:

As per the question:

Charges present on the corner of the triangle are same, Q =
`- 3.1* 10^(- 9) C`

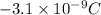
Since, its an equilateral triangle, distance between the charges, l = 0.50 m

Now,

The Coulomb force on a charge due to the other is:

`F_(C) = K(Q^(2))/(l^(2))`

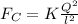
where

K = Coulomb constant =
`9* 10^(9) C^(2)/m^(2)`

`F_(C) = (9* 10^(9))((3.1* 10^(- 9))^(2))/(0.5^(2))`

`F_(C) = 111.6 N`

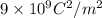
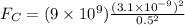
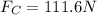
The the net force on the charges in an equilateral triangle on all the charges due to each other:

`F_(eq) = √(3)F_(C) = √(3)* 111.6 = 193.29 N`