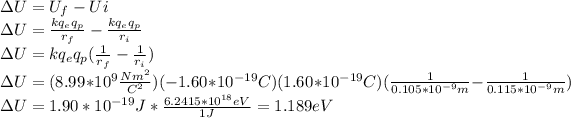Question

Many chemical reactions release energy. Suppose that at the beginning of a reaction, an electron and proton are separated by 0.115 nm , and their final separation is 0.105 nm . How much electric potential energy was lost in this reaction (in units of eV)?

Answer 1

`1.189eV`

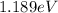
Step-by-step explanation:

The electric potential energy is the potential energy that results from the Coulomb force and is associated with the configuration of two or more charges. For an electron in the presence of an electric field produced by a proton, the electric potential energy is defined as:

`U=(kq_(e)q_(p))/(r)`

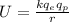
where
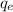`q_(e)` is the electron charge,
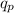`q_(p)` is the proton charge, r is the separation distance between the charges and k is the coulomb constant.

Knowing this, we can calculate how much electric potential energy was lost:

`\Delta U=U_(f)-U{i}\\\Delta U=(kq_(e)q_(p))/(r_(f))-(kq_(e)q_(p))/(r_(i))\\\Delta U=kq_(e)q_(p)((1)/(r_(f))-(1)/(r_(i)))\\\Delta U=(8.99*10^9(Nm^2)/(C^2))(-1.60*10^(-19)C)(1.60*10^(-19)C)((1)/(0.105*10^(-9)m)-(1)/(0.115*10^(-9)m))\\\Delta U=1.90*10^(-19)J*(6.2415*10^(18)eV)/(1J)=1.189eV`