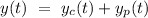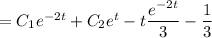Question

Use the variation of parameters method to solve the DR y" + y' - 2y = 1

Answer 1

`y(t)\ =\ C_1e^(-2t)+C_2e^t-t(e^(-2t))/(3)-(1)/(3)`

Explanation:

As given in question, we have to find the solution of differential equation

`y`

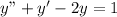
by using the variation in parameter method.

From the above equation, the characteristics equation can be given by

`D^2+D-2\ =\ 0`

`=>D=\ (-1+√(1^2+4* 2* 1))/(2* 1)\ or\ (-1-√(1^2+4* 2* 1))/(2* 1)`

`=>\ D=\ -2\ or\ 1`

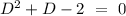
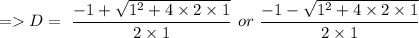
Since, the roots of characteristics equation are real and distinct, so the complementary function of the differential equation can be by

`y_c(t)\ =\ C_1e^(-2t)+C_2e^t`

Let's assume that

`y_1(t)=e^(-2t)`
`y_2(t)=e^t`

`=>\ y'_1(t)=-2e^(-2t)`
`y'_2(t)=e^t`

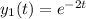
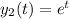
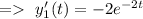
and g(t)=1

Now, the Wronskian can be given by

`W=y_1(t).y'_2(t)-y'_1(t).y_2(t)`

`=e^(-2t).e^t-e^t(-e^(-2t))`

`=e^(-t)+2e^(-t)`

`=3e^(-t)`

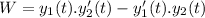
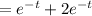
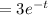
Now, the particular solution can be given by

`y_p(t)\ =\ -y_1(t)\int{(y_2(t).g(t))/(W)dt}+y_2(t)\int{(y_1(t).g(t))/(W)dt}`

`=\ -e^(-2t)\int{(e^t.1)/(3.e^(-t))dt}+e^(t)\int{(e^(-2t).1)/(3.e^(-t))dt}`

`=\ -e^(-2t)\int{(1)/(3)dt}+(e^t)/(3)\int{e^(-t)dt}`

`=(-e^(-2t))/(3).t-(1)/(3)`

`=-t(e^(-2t))/(3)-(1)/(3)`

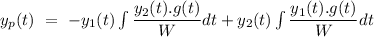
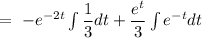
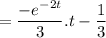
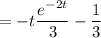
Now, the complete solution of the given differential equation can be given by

`y(t)\ =\ y_c(t)+y_p(t)`

`=C_1e^(-2t)+C_2e^t-t(e^(-2t))/(3)-(1)/(3)`