Question

(a) Find all points where the function f(z) = (x^2+y^2-2y)+i(2x-2xy) is differentiable, and compute the derivative at those points.

Answer 1

The given function is differentiable at y = 1.

At y = 1, f'(z) = 0

Explanation:

As per the given question,

`f(z)\ = (x^(2)+y^(2)-2y)+i(2x - 2xy)`

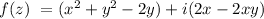
Let z = x + i y

Suppose,

`u(x,y) = x^(2)+y^(2)-2y`

`v(x,y) = 2x - 2xy`

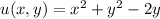
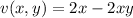
On computing the partial derivatives of u and v as:

`u'_(x) =2x`

`u'_(y)=2y -2`

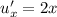
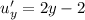
And

`v'_(x) =2-2y`

`v'_(y)=-2x`

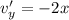
According to the Cauchy-Riemann equations

`u'_(x) =v'_(y) \ \ \ \ \ \ \ and\ \ \ \ \ \ u'_(y) = -v'_(x)`

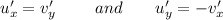
Now,

`(u'_(x) =2x) \\eq (v'_(y)=-2x)`

`(u'_(y)=2y -2) \ = \ (- v'_(x) =-(2-2y) =2y-2)`

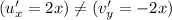
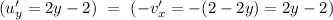
Therefore,

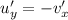`u'_(y)=- v'_(x)` holds only.

This means,

2y - 2 = 0

⇒ y = 1

Therefore f(z) has a chance of being differentiable only at y =1.

Now we can compute the derivative

`f'(z)=(1)/(2)[(u'_(x)+iv'_(x))-i(u'_(y)+iv'_(y))]`

`f'(z) =(1)/(2)[(2x+i(2-2y))-i(2y-2+i(-2x))]`

`f'(z) = i(2-2y)`

At y = 1

f'(z) = 0

Hence, the required derivative at y = 1 , f'(z) = 0