Answer:
The system will have no solution when
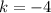 and
and
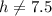 .
.
Explanation:
We can find these values by the Gauss-Jordan Elimination method.
The Gauss-Jordan elimination method is done by transforming the system's augmented matrix into reduced row-echelon form by means of row operations.
We have the following system:
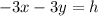
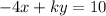
This system has the following augmented matrix:
![\left[\begin{array}{ccc}-3&-3&h\\-4&k&10\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/1tz1xxphrs0p8xwl540yb0id7u6kv3t60k.png)
The first thing i am going to do is, to help the row reducing:
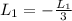
Now we have
![\left[\begin{array}{ccc}1&1&-(h)/(3)\\-4&k&10\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/9umb5b6ytsjlk2s45cm7x7xjrupez4rb8o.png)
Now I want to reduce the first row, so I do:

So:
![\left[\begin{array}{ccc}1&1&-(h)/(3)\\0&k+4&10 - (4h)/(3)\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/ladcidwiec9qpsjgwf7ar644nlcc8bvm07.png)
From the second line, we have
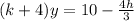
The system will have no solution when there is a value dividing 0, so, there are two conditions:
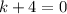 and
and
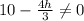
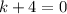
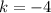
...
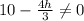
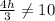
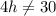

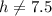
The system will have no solution when
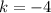 and
and
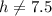 .
.