Answer:
The value of x is 2
Explanation:
* Lets explain how to find a distance between 2 points
- If the endpoints of a segment are
 and
and
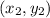 is
is

- Triangle ABC has a perimeter of 12 units
∵ The perimeter of any triangle is the sum of lengths of its sides
∴ P Δ ABC = AB + BC + AC
* Lets find the length of the three sides
∵ A = (x , 2) , B = (2 , -2) , C = (-1 , 2)
∵
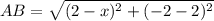
∴
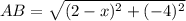
∴
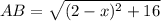
∵
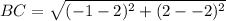
∴
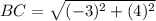
∴
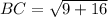
∴
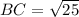
∴ BC = 5
∵
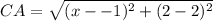
∴
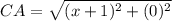
∴
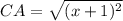
- The √ is canceled by power 2
∴ CA = (x + 1)
∵ AB + BC + CA = 12
∴
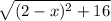 + 5 + (x + 1) = 12
+ 5 + (x + 1) = 12
- Add 5 and 1
∴
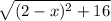 + 6 + x = 12
+ 6 + x = 12
- subtract 6 and x from both sides
∴
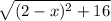 = (6 - x)
= (6 - x)
- To cancel (√ ) square the two sides
∴ (2 - x)² + 16 = (6 - x)²
- Simplify the two sides
∴ [(2)(2) + (2)(2)(-x) + (-x)(-x)] + 16 = (6)(6) + (2)(6)(-x) + (-x)(-x)
∴ 4 - 4x + x² + 16 = 36 - 12x + x²
- Subtract x² from both sides
∴ 20 - 4x = 36 - 12x
- Add 12x to both sides and subtract 20 from both sides
∴ 12x - 4x = 36 - 20
∴ 8x = 16
- Divide both sides by 8
∴ x = 2
* The value of x is 2