Question

A trebuchet was a hurling machine built to attack the walls of a castle under siege. A large stone could be hurled against a wall to break apart the wall. The machine was not placed near the wall because then arrows could reach it from the castle wall. Instead, it was positioned so that the stone hit the wall during the second half of its flight. Suppose a stone is launched with a speed of v0 = 25.0 m/s and at an angle of θ0 = 41.0°. What is the speed of the stone if it hits the wall (a) just as it reaches the top of its parabolic path and (b) when it has descended to half that height? (c) As a percentage, how much faster is it moving in part (b) than in part (a)?

Answer 1

(a) 18.9 m/s

The motion of the stone consists of two independent motions:

- A horizontal motion at constant speed

- A vertical motion with constant acceleration (
`g=9.8 m/s^2`) downward

We can calculate the components of the initial velocity of the stone as it is launched from the ground:

`u_x = v_0 cos \theta = (25.0)(cos 41.0^(\circ))=18.9 m/s\\u_y = v_0 sin \theta = (25.0)(sin 41.0^(\circ))=16.4 m/s`

The horizontal velocity remains constant, while the vertical velocity changes due to the acceleration along the vertical direction.

When the stone reaches the top of its parabolic path, the vertical velocity has became zero (because it is changing direction): so the speed of the stone is simply equal to the horizontal velocity, therefore

`v=18.9 m/s`

(b) 22.2 m/s

We can solve this part by analyzing the vertical motion only first. In fact, the vertical velocity at any height h during the motion is given by

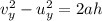`v_y^2 - u_y^2 = 2ah` (1)

where

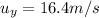`u_y = 16.4 m/s` is the initial vertical velocity

`v_y` is the vertical velocity at height h

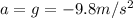`a=g=-9.8 m/s^2` is the acceleration due to gravity (negative because it is downward)

At the top of the parabolic path,
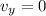`v_y = 0`, so we can use the equation to find the maximum height

`h_(max) = (-u_y^2)/(2a)=(-(16.4)^2)/(2(-9.8))=13.7 m`

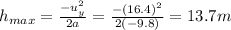
So, at half of the maximum height,

`h = (13.7)/(2)=6.9 m`

And so we can use again eq(1) to find the vertical velocity at h = 6.9 m:

`v_y = √(u_y^2 + 2ah)=√((16.4)^2+2(-9.8)(6.9))=11.6 m/s`

And so, the speed of the stone at half of the maximum height is

`v=√(v_x^2+v_y^2)=√(18.9^2+11.6^2)=22.2 m/s`

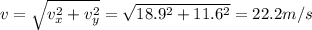
(c) 17.4% faster

We said that the speed at the top of the trajectory (part a) is

`v_1 = 18.9 m/s`

while the speed at half of the maximum height (part b) is

`v_2 = 22.2 m/s`

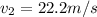
So the difference is

`\Delta v = v_2 - v_2 = 22.2 - 18.9 = 3.3 m/s`

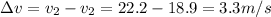
And so, in percentage,

`(\Delta v)/(v_1) \cdot 100 = (3.3)/(18.9)\cdot 100=17.4\%`

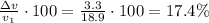
So, the stone in part (b) is moving 17.4% faster than in part (a).