Answer with Step-by-step explanation:
Let S be a semi-group.
Semi group: It is that set of elements which satisfied closed property and associative property.
We have to prove that S is a group if and only if the following condition hold'
1.S has left identity -There exist an element
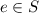 such that ea=a for all
such that ea=a for all

2.Each element of S has a left inverse - for each
 , there exist an element
, there exist an element
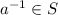 such that
such that

1.If there exist an element
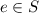 such that ea=a for all
such that ea=a for all

Then , identity exist in S.
2.If there exist left inverse for each

Then, inverse exist for every element in S.
All properties of group satisfied .Hence, S is a group.
Conversely, if S is a group
Then, identity exist and inverse of every element exist in S.
Identity exist: ea=ae=a
Inverse exist:
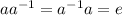
Hence, S has a left identity for every element

and each element of S has a left inverse .
Hence, proved.