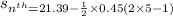Question

A car traveling 77 km/h slows down at a constant 0.45 m/s^2 just by "letting up on the gas." --Part a : Calculate the distance the car coasts before it stops.

--Part b: Calculate the time it takes to stop.
--Part c: Calculate the distance it travels during the first second.
--Part d: Calculate the distance it travels during the fifth second. Need help with all parts A-D, please show all work and formulas used.

Answer 1

(a) 508.37 m

(b) 47.53 s

(c) 21.165 m

(d) 19.365 m

Step-by-step explanation:

initial velocity, u = 77 km/h = 21.39 m/s

acceleration, a = - 0.45 m/s^2

(a) final velocity, v = 0

Let the distance traveled is s.

Use third equation of motion

`v^(2)=u^(2)+2as`

`0^(2)=21.39^(2)-2 * 0.45 * s`

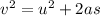
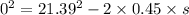
s = 508.37 m

(b) Let t be the time taken to stop.

Use first equation of motion

v = u + at

0 = 21.39 - 0.45 t

t = 47.53 s

(c) Use the formula for the distance traveled in nth second

`s_{n^(th)=u+(1)/(2)a\left ( 2n-1 \right )}`

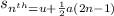
where n be the number of second, a be the acceleration, u be the initial velocity.

put n = 1, u = 21.39 m/s , a = - 0.45m/s^2

`s_{n^(th)=21.39-(1)/(2)* 0.45\left ( 2* 1-1 \right )}`

`s_{n^(th)=21.165m`

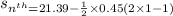
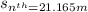
(d) Use the formula for the distance traveled in nth second

`s_{n^(th)=u+(1)/(2)a\left ( 2n-1 \right )}`

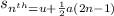
where n be the number of second, a be the acceleration, u be the initial velocity.

put n = 5, u = 21.39 m/s , a = - 0.45m/s^2

`s_{n^(th)=21.39-(1)/(2)* 0.45\left ( 2* 5-1 \right )}`

`s_{n^(th)=19.365m`