Question

An insulated Thermos contains 134 g of water at 70.7°C. You put in a 13.8 g ice cube at 0.00°C to form a system of ice + original water. The specific heat of liquid water is 4190 J/kg*K; and the heat of fusion of water is 333 kJ/kg. What is the net entropy change of the system from then until the system reaches the final (equilibrium) temperature?

Answer 1

`\Delta s\ =\ 21.33\ J/K`

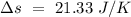
Step-by-step explanation:

Given,

• Mass of the ice =
  `m_i\ =\ 13.8\ kg\ =\ 0.0138\ kg`
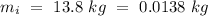
• Temperature of the ice =
  `T_i\ =\ 0^o\ C`
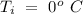
• Mass of the original water =
  `m_w\ =\ 134\ g\ =\ 0.134\ kg`
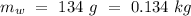
• Temperature of the original water =
  `T_w\ =\ 70.0^o\ C`
• Specific heat of water =
  `S_w\ =\ 4190\ J/kg K`
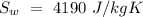
• Latent heat of fusion of ice =
  `L_f\ =\ 333\ kJ/kg`

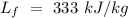
Let T be the final temperature of the mixture,

Therefore From the law of mixing, heat loss by the water is equal to the heat gained by the ice,

`m_iL_f\ +\ m_is_w(T_f\ -\ 0)\ =\ m_ws_w(T_w\ -\ T_f)\\\Rightarrow 333000* 0.0138\ +\ 0.0138* 4190T_f\ =\ 0.134* 4190*(70.7\ -\ T_f)\\\Rightarrow 4595.4\ +\ 57.96T_f\ =\ 39789.96\ -\ 562.8T_f\\\Rightarrow 620.76T_f\ =\ 35194.56\\\Rightarrow T_f\ =\ (35194.56)/(620.76)\\\Rightarrow T_f\ =\ 56.69^o\ C`

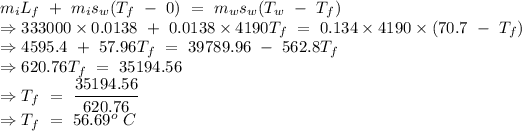
Now, We know that,

Change in the entropy,

`\Delta s\ =\ s_f\ -\ s_i\ =\ (Q)/(T)\\\Rightarrow \displaystyle\int_(s_i)^(s_f) ds\ =\ \displaystyle\int_(T_i)^(T_f)(msdT)/(T)\\\Rightarrow \Delta s =\ ms \ln \left ((T_i)/(T_f)\ \right )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,eqn (1)`

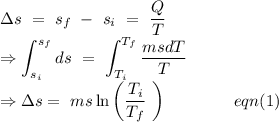
Now, change in entropy for the ice at 0^o\ C to convert into 0^o\ C water.

`\Delta s_1\ =\ (Q)/(T)\\\Rightarrow \Delta s_1\ =\ (m_iL_f)/(T)\ =\ (0.0138* 333000)/(273.15)\ =\ 16.82\ J/K.`

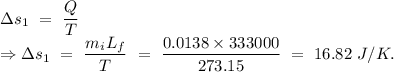
Change in entropy of the water converted from ice from
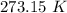`273.15\ K` to water 330.11 K water.

From the equation (1),

`\therefore \Delta s_2\ =\ ms \ln \left ((T_i)/(T_f)\ \right )\\\Rightarrow \Delta s_2\ =\ 0.0138* 4190* \ln \left ((273.15)/(330.11)\ \right )\\\Rightarrow \Delta s_2\ =\ 6.88\ J/K`

Change in entropy of the original water from the temperature 342.85 K to 330.11 K

From the equation (1),

`\therefore \Delta s_3\ =\ ms \ln \left ((T_i)/(T_f)\ \right )\\\Rightarrow \Delta s_3\ =\ 0.134* 4190* \ln \left ((330.11)/(343.85) \right )\\\Rightarrow \Delta s_3\ =\ -2.36\ J/K`

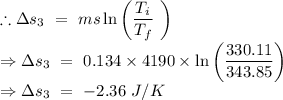
Total entropy change =
`\Delta s\ =\ \Delta s_1\ +\ \Delta s_2\ +\ \Delta s_3\\\Rightarrow \Delta s\ =\ (16.82\ +\ 6.88\ -\ 2.36)\ J/K\\\Rightarrow \Delta s\ =\ 21.33\ J/K.`

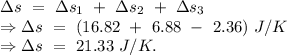
Hence, the change in entropy of the system form then untill the system reaches the final temperature is 21.33 J/K