Explanation:
a) Give two pairs which are in the relation
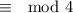 and two pairs that are not.
and two pairs that are not.
As stated before, a pair
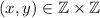 is equal mod m (written
is equal mod m (written
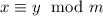 ) if
) if
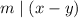 . Then:
. Then:
- x=0 and y=4 is an example of a pair
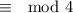
- x=0 and y=1 is an example of a pair
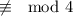
b) Show the
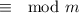 is an equivalence relation.
is an equivalence relation.
An equivalence relation is a binary relation that is reflexive, symmetric and transitive.
By definition
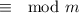 is a binary relation. Observe that:
is a binary relation. Observe that:
- Reflexive. We know that, for every m,
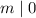 . Then, by definition,
. Then, by definition,
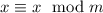 .
. - Symmetry. It is clear that, given x,y and m such that
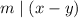 , then
, then
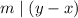 . Therefore
. Therefore
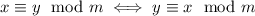
- Transitivity. Let x,y,z and m such that
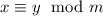 and
and
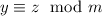 . Then,
. Then,
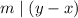 and
and
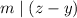 . Therefore:
. Therefore:
![m\mid [(y-x)+(z-y)] \implies m\mid (z-x) \implies x\equiv z \mod m](https://img.qammunity.org/2020/formulas/mathematics/college/72fl3k8oj3w8lym6jdspyom6geojopd7ft.png) .
.
In conclusion,
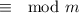 defines an equivalence relation.
defines an equivalence relation.