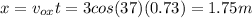Answer:
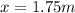
Step-by-step explanation:
From the exercise we have that
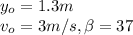
To find how far from the edge of the piano does the cat strike the floor, we need to calculate its time first
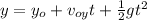
At the end of the motion y=0m
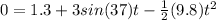
Solving for t
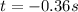 or
or
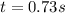
Since the time can't be negative the answer is t=0.73
Knowing that we can calculate how far does the cat strike the floor