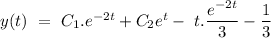Answer:
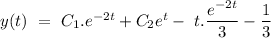
Explanation:
Given differential equation is,
y"+y'-2y=1
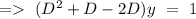
To find the complementary function we will write,
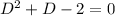
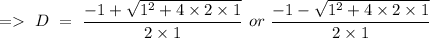
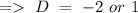
Hence, the complementary function can be given by
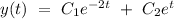
Let's say,
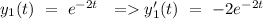
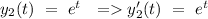
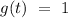
Wronskian can be given by,
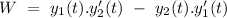

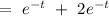
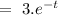
Now, the particular integral can be given by
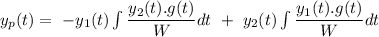
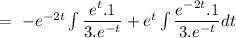
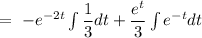
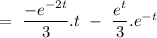
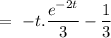
Hence, the complete solution can be given by