Question

Solve the differential equation x^2 y"-xy' +y 0

Answer 1

`y(x)\ =\ √(x)[C_1cos(√(3))/(2)logx+C_2sin(√(3))/(2)logx]`

Explanation:

Given differential equation is

`x^2y` (1)

Let's assume that

`x=e^t`

`=>\ t\ =\ logx`

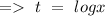
then,

`(dx)/(dt)=e^t`

`and\ (d^2x)/(dt^2)=e^t`

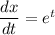
We can write,

`(dy)/(dx)=(dy)/(dt).(dt)/(dx)`

`=e^(-t)(dy)/(dt)`

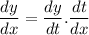
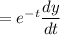
Similarly,

`(d^2y)/(dt^2)=(d^2y)/(dt^2).(dt^2)/(dx^2)`

`=e^(-2t).(d^2y)/(dt^2)`

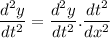
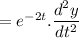
Putting these values in equation (1), we will get

`e^(2t).e^(-2t).(d^y)/(dt^2)-e^t.e^(-t)(dy)/(dt)+y=0`

`=>(d^2y)/(dt^2)-(dy)/(dt)+y=0`

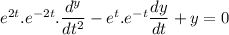
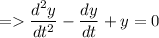
So, the characteristics equation can be given as

`D^2-D+1=0`

`=>D\ =\ (1+√(1-4))/(2)\ or\ (1-1√(1-4))/(2)`

`=>D=\ (1)/(2)+i(√(3))/(2)\ or\ (1)/(2)-i(√(3))/(2)`

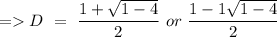
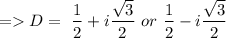
Hence, the general solution of the equation can be give by

`y(t)\ =\ e^{(t)/(2)}[C_1cos(√(3))/(2)t+C_2sin(√(3))/(2)t]`

Now, by putting the value of t in above solution, we will have

`y(x)\ =\ e^{(1)/(2)logx}[C_1cos(√(3))/(2)logx+C_2sin(√(3))/(2)logx]`

`y(x)=\ √(x)[C_1cos(√(3))/(2)logx+C_2sin(√(3))/(2)logx]`

Hence, the solution of above given differential equation can be given by

`y(x)=\ √(x)[C_1cos(√(3))/(2)logx+C_2sin(√(3))/(2)logx]`