Question

If the demand function for a commodity is given by the equation

p^2 + 16q = 1400

and the supply function is given by the equation

700 − p^2 + 10q = 0,

find the equilibrium quantity and equilibrium price. (Round your answers to two decimal places.)

equilibrium quantity
equilibrium price $

Answer 1

Equilibrium quantity = 26.92

Equilibrium price is $31.13

Explanation:

Given :Demand function :
`p^2 + 16q = 1400`

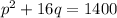
Supply function :
`700 -p^2 + 10q = 0`

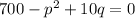
To Find : find the equilibrium quantity and equilibrium price.

Solution:

Demand function :
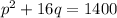`p^2 + 16q = 1400` --A

Supply function :
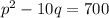`p^2-10q=700` ---B

Now to find the equilibrium quantity and equilibrium price.

Solve A and B

Subtract B from A

`p^2-10q -p^2-16q=700-1400`

`-26q=-700`

`26q=700`

`q=(700)/(26)`

`q=26.92`

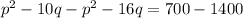
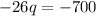
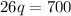
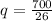
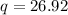
So, equilibrium quantity = 26.92

Substitute the value of q in A

`p^2 + 16(26.92) = 1400`

`p^2 + 430.72 = 1400`

`p^2 = 1400- 430.72`

`p^2 = 969.28`

`p = √(969.28)`

`p = 31.13`

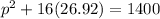
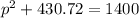
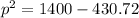
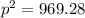
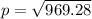
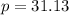
So, equilibrium price is $31.13